---

Spectroscopic Geometry

The spectroscopic geometry is defined similarily to the neutral beam. It is defined by the lens position in machine coordinates and an optical axis. The volume of the sightline is assumed to be cylindrical with radius, spot_size.

If mirrors are present then the apparent positions of the lens as seen from the plasma are used. Additionally, mirrors reflect the sigma and pi Stark lines differently due to a difference in polarization. The experimentally determined ratio of the intensties of the sigma and pi lines, sigma_pi, is used to correct for this. If there are no mirrors then sigma_pi is set to 1.0 .

The full geometry specification is given below.

Variable	Type	Rank	Dimensions	Units	Description
nchan	Int32	0	NA	NA	Number of channels
system	String	0	NA	NA	Name of the spectrocopic system(s)
data_source	String	0	NA	NA	Source of the spectral geometry data
id	String	1	[nchan]	NA	Channel ID
radius	Float64	1	[nchan]	cm	Line of sight radius at midplane or tangency point
lens	Float64	2	[3,nchan]	cm	Lens location in machine coordinates
axis	Float64	2	[3,nchan]	NA	Optical axis/direction of the lines of sight
spot_size	Float64	1	[nchan]	cm	Radius of the collecting volume
sigma_pi	Float64	1	[nchan]	NA	Ratio of the intensities of the sigma and pi stark lines

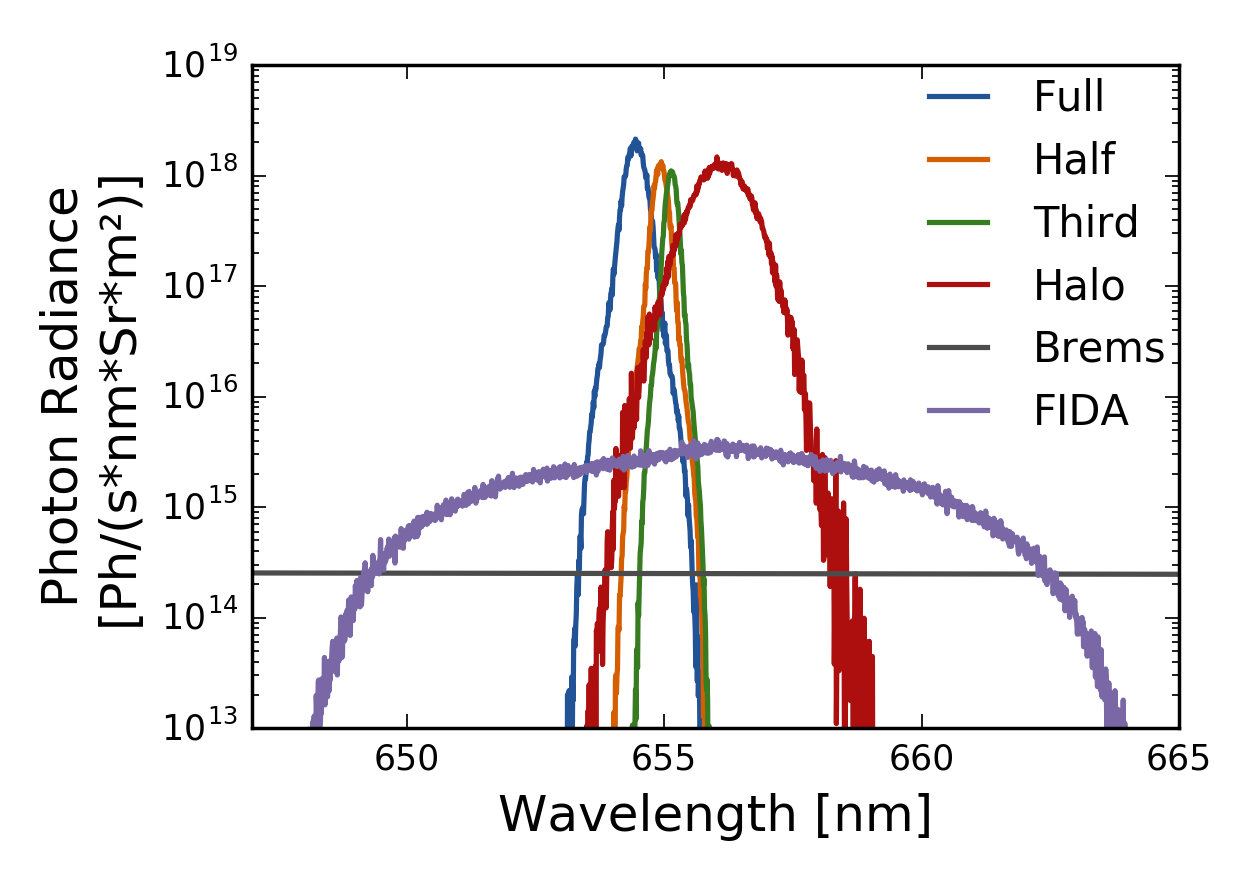
Types of Spectra

FIDASIM can calculate the following spectra

• Bremsstrahlung
• Beam Emission (BES: Full, Half, Third)
• Halo Emission
• Fast-ion D-$\alpha$ (FIDA)

Bremsstrahlung

The largest source of background emission is visible bremsstrahlung. The local bremsstrahlung emissivity per unit wavelength is given by

$$\frac{dN_B}{d\lambda} = 7.57 \times 10^{-9} \, g \, \frac{n_e^2 \, Z_{eff}}{\lambda \, T_e^{1/2}} e^{-hc/\lambda \,T_e}$$

where $\lambda$ is the wavelength in angstroms, $n_e$ is the electron density in $cm^{-3}$, $T_e$ is the electron temperature in eV. The gaunt factor, $g$, depends on $T_e$ and $Z_{eff}$. It can be approximated by

$$g = 5.542 - (3.108 - \ln(T_e/1000))(0.6905 - 0.1323/Z_{eff})$$

To calculate the total emission "seen" by the line of sight the the local emissivity is integrated over the line of sight.

Emission by Neutrals

There are two processes in which neutrals can emit light: Excitation and Charge Exchange.

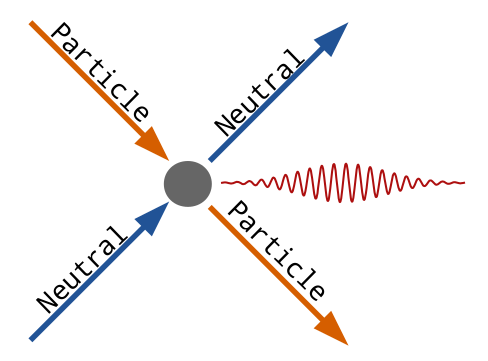
Excitation is the primary method in which beam neutrals emit light (BES). In short, a neutral particle collides with a charged particle, exciting into a higher energy ($n=3$) state. When the neutral particle relaxes ($n: 3 \rightarrow 2$) it emits a doppler shifted (656.1 nm) photon.

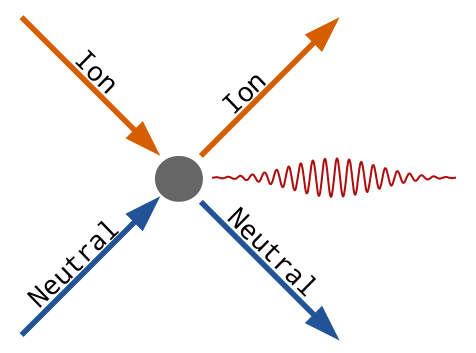
Charge Exchange is the process by which the Halo and FIDA light is created. In a charge exchange reaction a thermal (Halo) or fast (FIDA) ion steals a electron from a neutral particle. The newly created neutral is born in an excited ($n=3$ state and like the collisionally excited neutral it relaxes to a lower energy state (\n=2) and emits a doppler shifted (656.1 nm) photon.

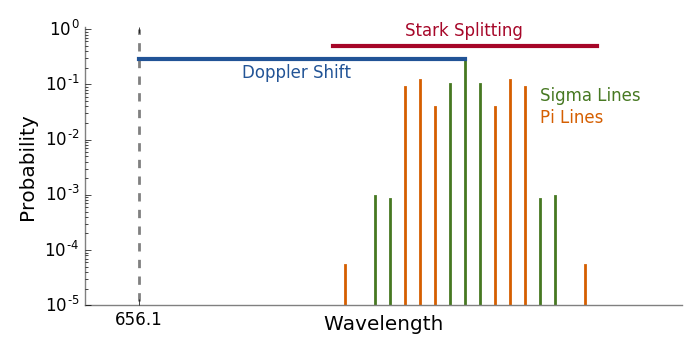
The motion of a ion in a magnetic field induces an electric field which causes Stark Spitting of the the atoms energy levels. Most atoms the strength of the Stark effect is quadratic in low electric fields and linear for strong electric fields. Usually atoms never the linear regime but, due to degenerency between states of different angular momentum, hydrogenic atoms exhibit a linear Stark effect. The linear Stark energy component shifts are given by the following equations.

$$\Delta \mathcal{E} = 3nk\frac{E}{Ze/4\pi\epsilon_0a_0^2}R_y\;\, \mathrm{for} \;\,k=0,\pm 1,\dots,\pm (n-1)$$

As seen from the above equation, each energy level is split into $2n-1$ parts. For the Balmer-alpha transition, this creates 15 distinct transitions from the $n=3 \rightarrow 2$ state.

The relative intensity of the different Stark lines is given by

$$I_{rel}(i) = S_I(i)\,(1 \pm (\vec{v}_{ph} \cdot \vec{E})^2)$$ $$I_{rel}(i) = \frac{I_{rel}(i)}{\sum_i I_{rel}(i)}$$

where positive and negative sums refer to $\sigma$ and $\pi$ lines respectively and $S_I$ are the calculated relative Stark intensities for each transition given by

$$S_I = [1, 18, 16, 1681, 2304, 729, 1936, 5490, 1936, 729, 2304, 1681, 16, 18, 1]$$

Relevant Namelist Settings

• calc_fida: Calculate FIDA spectra
• calc_brems: Calculate Bremsstrahlung
• calc_bes: Calculate Beam Emission and Halo
• dump_dcx: Dump DCX spectra
• n_fida: Number of Monte Carlo particles used in FIDA spectra calculation
• n_nbi: Number of Monte Carlo particles used in BES spectra calculation
• n_dcx and n_halo: Number of particles used in Halo spectra calculation
• nlambda: Number of wavelength bins
• lambdamin: Minimum wavelength [nm]
• lambdamax: Maximum wavelength [nm]

Fortran References

• bremsstrahlung: Calculates Bremsstrahlung
• spectrum: Calculates Doppler shift and Stark splitting.
• ndmc: Calculates BES spectra
• dcx: Calculates DCX neutrals contribution to the Halo spectra
• halo: Calculates thermal neutrals contribution to the Halo Spectra
• fida_f: Calculates FIDA light using a distribution function
• fida_mc: Calculates FIDA light using a particle distribution