---

Beam Grid

The neutrals densities calculated by FIDASIM are stored in a 3D grid. FIDASIM requires that the grid be axis-aligned to easily track particles through the grid. However, it is extremely useful to be able to align the grid along the beam centerline. To facilitate this FIDASIM allows the user to define arbitrary Cartesian coordinate system (beam grid coordinates) that all calculations are done in.

FIDASIM uses Tait-Bryan rotation angles (alpha,beta,gamma) to define a intrinsic rotation matrix, $R$, that is used to transform from beam grid coordinates(xyz) to machine coordinates(uvw) $$\mathrm{uvw = R \cdot xyz + origin}$$ If the rotation angles and origin are set to zero then the rotation matrix is the Identity matrix and the coordinate system is identical to machine coordinates (Standard Cartesian).

Understanding these variables can be difficult and can best be described by an example.

1. With your right hand point your index finger pointing in the +x direction with your middle finger and thumb pointing in the +y and +z direction respectively.
2. Rotate about your thumb (z-axis) by alpha (ccw = +angle, cw = -angle)
3. Rotate about your middle finger (y'-axis) by beta
4. Rotate about your index finger (x"-axis) by gamma
5. Move your right hand to the origin
6. Define (x|y|z)_(min|max) by this coordinate system with your index finger being the new +x-axis

The beam grid is defined in the namelist file ([runid]_inputs.dat) and are defined as follows

Variable	Type	Rank	Dimensions	Units	Description
nx	Int16	0	NA	NA	Number of cells in the X direction
ny	Int16	0	NA	NA	Number of cells in the Y direction
nz	Int16	0	NA	NA	Number of cells in the Z direction
xmin	Float64	0	NA	cm	Minimum X value in beam grid coordinates
xmax	Float64	0	NA	cm	Maximum X value in beam grid coordinates
ymin	Float64	0	NA	cm	Minimum Y value in beam grid coordinates
ymax	Float64	0	NA	cm	Maximum Y value in beam grid coordinates
zmin	Float64	0	NA	cm	Minimum Z value in beam grid coordinates
zmax	Float64	0	NA	cm	Maximum Z value in beam grid coordinates
alpha	Float64	0	NA	rad	Tait-Bryan rotation angle about z-axis
beta	Float64	0	NA	rad	Tait-Bryan rotation angle about y'-axis
gamma	Float64	0	NA	rad	Tait-Bryan rotation angle about x"-axis
origin	Float64	1	[3]	cm	Beam grid origin in Machine Coordinates

Neutral Beam Geometry

A neutral beam is defined by a source position and an axis such that a position along the beam centerline is defined as $$\vec{C}(t) = \vec{s} + \vec{a} \cdot t$$ where $\vec{C}(t)$ is the position along the centerline parameterized by $t$, $\vec{s}$ is the source position in machine coordinates, and $\vec{a}$ is the axis.

The ion source is defined by its shape (circular or rectangular), size (half width and height), focal length (vertical and horizontal), and divergence (energy dependent). The neutral beam is simulated by firing particles from random positions on the source plate. The trajectory of the particles is determined by the following equations (+x into the plasma) $$v_x = 1$$ $$v_y = -\frac{y_s}{f_y} + \tan(\mathcal{N}(0,\beta_y^2))$$ $$v_z = -\frac{z_s}{f_z} + \tan(\mathcal{N}(0,\beta_z^2))$$ where $y_s$ and $z_s$ are random positions on the source plate in the horizontal and vertical directions respectively, $f_{y/z}$ are the focal lengths, and $\beta_{y/z}$ are the divergences. Examples of different trajectories are shown below.

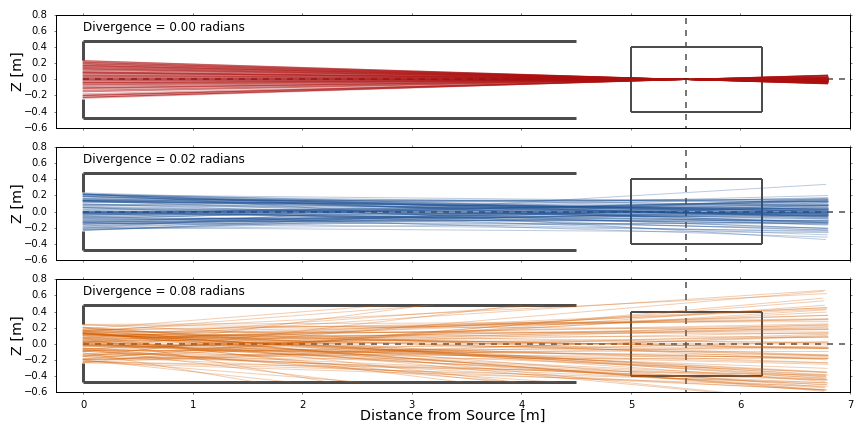
Not shown above are the beam aperture(s) which collimates the neutral beam. Apertures are represented in FIDASIM by their shape (circular or rectangular), size (half width and height), offsets relative to the +x aligned beam centerline, and their distance from the source grid. It is assumed that the plane of the aperture(s) is parallel to the plane of the source grid. The routine nubeam_geometry.pro(IDL) can be used to easily generate the NBI geometry from the TRANSP/NUBEAM beam definition.

FIDASIM reads in the neutral beam geometry from a HDF5 file ([runid]_geometry.h5) that has the group nbi with the following datasets

Variable	Type	Rank	Dimensions	Units	Description
name	String	0	NA	NA	Name of the neutral beam
shape	Int16	0	NA	NA	Shape of the beam source grid (1=rect or 2=circ)
data_source	String	0	NA	NA	Source of the neutral beam geometry
src	Float64	1	[3]	cm	Position of the source grid in machine coordinates
axis	Float64	1	[3]	NA	Direction of the beam center line
widy	Float64	0	NA	cm	Source grid half-width in the horizontal direction
widz	Float64	0	NA	cm	Source grid half-height in the vertical direction
divy	Float64	1	[3]	rad	Horizontal beam divergence
divz	Float64	1	[3]	rad	Vertical beam divergence
focy	Float64	0	NA	cm	Horizontal focal length
focz	Float64	0	NA	cm	Vertical focal length
naperture	Int16	0	NA	NA	Number of apertures
ashape	Int16	1	[naperture]	NA	Shape of the aperture(s) (1=rect or 2=circ)
awidy	Float64	1	[naperture]	cm	Half-width of the aperture(s)
awidz	Float64	1	[naperture]	cm	Half-height of the aperture(s)
aoffy	Float64	1	[naperture]	cm	Horizontal (y) offset of the aperture(s) relative to the +x aligned beam centerline
aoffz	Float64	1	[naperture]	cm	Vertical (z) offset of the aperture(s) relative to the +x aligned beam centerline
adist	Float64	1	[naperture]	cm	Distance from the center of the beam source grid to the aperture(s) plane

Neutral Beam Density

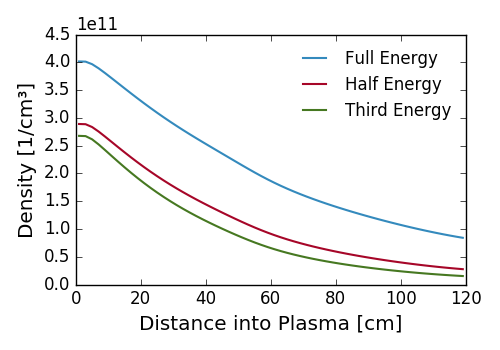
Neutral Hydrogen beams usually contain atoms with different energies: $H(E_{inj})$ (Full), $H(E_{inj}/2)$ (Half),$H(E_{inj}/3)$ (Third). This splitting of energy is due to multiple atomic and molecular species being accelerated to the same kinetic energy, $E_{inj}$. Each beam species will attenuate differently into the plasma and need to be treated separetely. It is assumed that each neutral is in the ground state with initial flux given by $$F_i(n=1) = \frac{dN_i}{dt} = C_i \cdot \frac{dN_{tot}}{dt}$$ where $C_i$ is current fraction for the $i_{th}$ energy component and $dN_{tot}/dt$ is the total flux of neutrals given by $$\frac{dN_{tot}}{dt} = \frac{P_{inj}}{C_1 E_{inj}+ C_2 E_{inj}/2 + C_3 E_{inj}/3}$$ where $P_{inj}$ is the beam power.

Within each beam grid cell along the neutral trajectory the flux is modified using the collisional radiative model and the neutral density is calculated. The figure below illustrates the different beam attenuation profiles.

DCX and Halo Density

A secondary source of neutrals come from the charge exchange reaction between beam neutrals and thermal ions (DCX). After neutralization, the newly created thermal neutrals travel ballistically and charge exchange with other thermal ions creating more neutrals (Halo). This process is then repeated multiple times in a recursive fashion producing fewer and fewer neutrals. The effect of this process is a Halo of neutrals surrounding the neutral beam.

FIDASIM uses the following scheme to calculate the DCX+Halo contribution.

$\rm{DCX:\,\,\,} \quad H_{t_0}^+ + H_b \rightarrow H_{t_0} + H_b^+$

$\rm{Halo\,1:} \quad H_{t_1}^+ + H_{t_0} \rightarrow H_{t_1} + H_{t_0}^+$

$\rm{Halo\,2:} \quad H_{t_2}^+ + H_{t_1} \rightarrow H_{t_2} + H_{t_1}^+$

$\vdots$

$\rm{Halo\,n:} \quad H_{t_n}^+ + H_{t_{(n-1)}} \rightarrow H_{t_n} + H_{t_{(n-1)}}^+$

After a few iterations the halo density converges and the calculation ends.

Relevent Namelist Settings

• ab: Beam/Fast-ion mass [amu]
• pinj: Beam power [MW]
• einj: Beam Energy [keV]
• current_fractions: Current fractions
• load_neutrals: Load neutrals from file
• neutrals_file: Optional neutrals file
• dump_dcx: Optionally dump DCX density and spectra
• n_nbi: Number of NBI MC particles
• n_halo: Number of HALO MC particles
• n_dcx: Number of DCX MC particles
• calc_birth: Calculate birth profile (density & birth position and velocity)
• n_birth: Number of birth particles outputed

Fortran References

• xyz_to_uvw: Transforms a point from beam grid coordinates to machine coordinates
• uvw_to_xyz: Transforms a point from machine coordinates to beam grid coordinates
• mc_nbi: Generates beam neutral trajectory
• ndmc: Calculates neutral beam density
• dcx: Calculates DCX contribution
• halo: Calculates Halo contribution
• write_dcx: Writes DCX neutrals to file
• write_neutrals: Writes neutrals to file